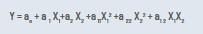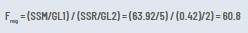- China declara que “ignorará” los “juegos de números arancelarios” de EE.UU.
- Beca PERUMIN: Más de 2180 jóvenes de 23 regiones del Perú postularon para acceder a las actividades de la Convención Minera
- Minem: el Algarrobo es el primer proyecto en priorizar el recurso hídrico en Perú
- MINEM: Cusco será la primera región del país con proyectos en energía rural trifásica
- Impulso a la equidad de género resaltó en Encuentro de Mujeres Líderes de Ferreycorp
Geometalurgia y estadística para procesamiento de minerales

I INTRODUCCIÓN
La caracterización mineralógica de zonas de minado es cada vez más importante para el procesamiento efectivo de los minerales; el concepto geometalurgico indica estudiar los tipos de frente de minado y sus posibles combinaciones para maximizar el beneficio metalúrgico.
El presente trabajo desarrolla un sistema de investigación metalúrgica de mezcla de dos tipos de mineral, con la finalidad de ser procesados en planta de flotación, este sistema usa la consistencia del análisis estadístico de un diseño experimental de segundo orden (Hexagonal), en el mismo, la variable principal es optimizada en un rango real entre 0 y 10% en peso del total de mineral procesado; la segunda variable es el tiempo de molienda que tiene un rango muy corto con la finalidad de que sirva solo de “variable de compañía” y efectivamente solo se optimize la primera variable.
Son ocho pruebas de flotación batch (seis del diseño Hexagonal y dos pruebas en el centro para determinar el error experimental), la función objetivo es recuperación de cobre, las condiciones variables de las pruebas de flotación batch será: (1) la mezcla de minerales y (2) el tiempo de molienda batch en minutos. El resto de parámetros tales como tiempos de flotación, acondicionamiento y dosificación de reactivos de flotación se mantienen constantes durante las ocho pruebas de flotación batch.
Con diseño experimental la mezcla de minerales se hace más consistente, de no aplicar este sistema, solo se intentará combinaciones imaginarias y no podrán ser analizadas con la prolijidad y alcance del análisis de regresión y valor estadístico F.
II BREVE MARCO TEÓRICO
En la etapa de selección de variables corresponde a investigar en la parte baja de la “cima” (que representa la función objetivo en tres dimensiones) y cuyo máximo se alcanzara estando alrededor de dicha “punta de cerro imaginario” en una etapa superior a la cual se llega con diseños de optimización de segundo orden y que generalmente se aplica para dos variables (diseño Hexagonal y Octogonal)
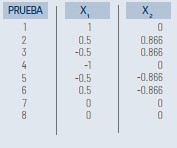
El modelo de diseño hexagonal consta de 6 pruebas y que codificadas están ubicadas en las coordenadas de un hexágono regular con centro en el origen (0,0) inscrito en una circunferencia de radio 1 y para realizar las pruebas se decodifica los valores y también se agregan por lo menos dos pruebas adicionales al centro con la finalidad de analizar el error experimental.
Abajo se encuentra la plantilla codificada de un diseño Hexagonal
El modelo de relación de una respuesta (Y) respecto de dos variables X1 y X2 es de segundo orden tiene la siguiente forma:
Las pruebas experimentales para determinar Y se realizan con los valores del rango de las dos variables, para encontrar los coeficientes es necesario hacer regresión con una plantilla ampliada
Es importante considerar que si los coeficientes de las variables elevadas al cuadrado son negativas ambas (a 11 y a22) estaremos ante una posibilidad de una respuesta máxima, si las dos son positivas estaremos frente a un mínimo y si los signos son diferentes se tendrá una “montura” que indica estar fuera de rango apropiado para continuar el proceso de optimización.
En cuanto al análisis estadístico de resultados se usa el estadístico F, que es una estimación de la comparación de varianzas y para la regresión si valor de F es (>) mayor que un valor de F de la tabla, la ecuación explica el evento en que los puntos están compensados alrededor de una curva.
Estimando el valor de F de falta de ajuste y si es menor que un F de tabla significará que los puntos están próximos a la curva. Ambas condiciones simultáneas validan la ecuación que determinara los valores óptimos.
III EJEMPLO DE APLICACIÓN
USO DEL DISEÑO HEXAGONAL PARA MEZCLA DE MINERALES CON ALTO CONTENIDO DE OXIDO DE COBRE
Se justifica este trabajo por la necesidad de encontrar la cantidad de mineral oxidado de cobre, que dosificada diariamente afectarían lo menos posible la recuperación metalúrgica de cobre.
Rangos de variables
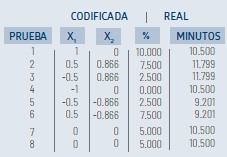
Plantilla Codificada y Real
La plantilla codificada del diseño hexagonal se coloca en valores reales, utilizando la siguiente formula de descodificacion :
Radio es la distancia del centro al extremo máximo de un rango real.
Explicación de las variables:
– La variable X1 escogida es el % de mineral de tajo que contiene mineral oxidado de cobre (MOxCu) respecto del mineral estándar común, los límites fueron inferior 0 (nada de este mineral especial) y superior 10% , que se determinó previamente como el máximo tonelaje que se podía extraer económicamente de dicho stock de mineral oxidado.
– La variable X2 es el grado de molienda, entre los límites 9 a 12 minutos como inferior y superior, esta molienda batch representaba K80 entre 175 y 185 micrones, este rango es corto y ajustado, la finalidad es que sirva solo como variable de “compañía”, ya que el único objetivo es evaluar la cantidad de mineral oxidado de cobre, se sabe que la flotación en ese rango de molienda prácticamente no cambia.
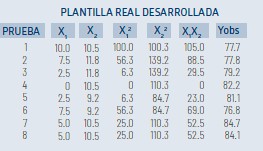
Para que los coeficientes de la regresión estén expresados en unidades reales, la plantilla del diseño hexagonal se conforma en valores reales como sigue:
La respuesta en recuperación de cobre figura en la última columna del cuadro anterior.
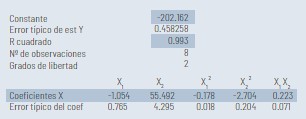
El resultado de la regresión es:
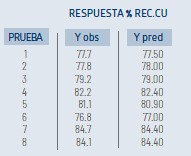
Los valores predichos según la regresión son:
ANÁLISIS ESTADISTICO DE RESULTADOS
Conformada La matriz para valores X1, X2, X1 2, X2 2, X1X2 al proceder la regresión para recuperación de cobre, se observa una correlación de 0.993 que significa que la ecuación de coeficientes expresa realmente el evento experimental para la recuperación cobre, además los coeficientes de los términos elevados al cuadrado ambos son negativos lo cual de acuerdo a la matriz hessiana adelanta que habrá un máximo en dicha función objetivo
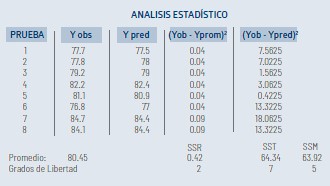
El cuadro siguiente contiene la información para el análisis estadístico para determinar el F de regresión y el valor F de falta de ajuste.
Los valores de la tabla anterior se explican del siguiente modo:
- En la primera columna figura el número de pruebas, se confirma seis pruebas (una por cada punta del hexágono y dos pruebas al centro, en total son ocho pruebas.
- La segunda columna contiene el resultado de recuperación de cobre en cada una de las ocho pruebas.
- La tercera columna es el cálculo de la respuesta Y cuando se aplica el resultado de regresión, es decir aplicando el valor constante y los coeficientes de regresión para cada fila de datos, se le denomina Ypred o predicho porque es el resultado de Y cuando se aplica la ecuación del modelo de regresión.
- La cuarta columna es el resultado de la diferencia del Y observado menos el Y predicho, elevado al cuadrado; la suma total de los ocho valores representan la suma de cuadrados residuales (SSR), en este caso es 0.42
- La quinta columna es la diferencia de la respuesta Y observado menos el valor promedio de todas las observaciones y elevadas al cuadrado; en este caso representa a la Suma de Cuadrados Totales (SST), pare este ejemplo corresponde 64.34
- A la derecha se tiene un valor denominado SSM, o Suma de Cuadrados del Modelo y está definido como la diferencia entre SST y SSR , el valor que corresponde es 64.34-0.42 = 63.92
- Un valor de F se calcula por comparación de varianzas, una varianza se determina dividiendo una suma de cuadrados entre los grados de libertad; por ejemplo los grados de libertad del SSR son los disponibles, según la regresión, se tiene 8 pruebas, descontar un grado de libertad por el termino constante y uno por cada uno de los cinco coeficientes de la ecuación de regresión, en total se ocuparon 6 grados de libertad y quedan 2 disponibles.
- En cuanto a los grados de libertad de la suma de cuadrados SST es el número de pruebas menos 1, si se tienen ocho pruebas el resultado de GL es 7
- Los grados de libertad del SSM son la diferencia entre grados de libertad de SST menos SSR, es decir 7-2 = 5
F DE LA REGRESIÓN
La comparación de varianzas tiene la siguiente relación:
Entonces el valor Freg = 60.8 que es mayor que el Ftabla para (5,2 grados de libertad, al 95% de confianza) 19,3
F DE FALTA DE AJUSTE
El termino SSF es la suma de cuadrados de la falta de ajuste resulta de la diferencia de SSR de todas la pruebas (0.42) menos la suma de cuadrados del error experimental SSE es decir la suma de lo que corresponde a las pruebas al centro (0.18), entonces SSF = 0.42-0.18 = 0.24
Los grados de libertad del SSE son el número de pruebas al centro menos uno, en este caso 2-1 =1
Los grados de libertad de SSF son el correspondiente a grados de libertad de SSR (2) menos los grados de libertad de SSE. Entonces G.L. de SSF es 2-1 = 1
Entonces el valor de F es la comparación de la varianza SSF/G.L. Dividido entre la varianza SSE/G.L.
El valor Ffajuste =1.33 es menor que el valor de tabla Ftabla = 18.1 (para 1,1 grados de libertad y 95% de confianza)
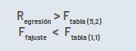
Con el análisis anterior queda demostrada la consistencia estadística del estudio porque se cumplen dos condiciones:
Calculo de valores de variables para máxima recuperación de cobre
La función matemática o modelo obtenida por regresión es la siguiente:
Aplicando el concepto de derivados parciales igualando a cero y resolviendo simultáneamente.
Los valores de X1 = 3.56% y X2 =10.41 minutos (correspondiente a K80 = 180 micrones), otorgan un máximo de recuperación de cobre.
Entonces para un procesamiento diario de 140, 000 toneladas, podría alimentarse el 3.56% ó 5000 toneladas de mineral oxidado de cobre por dia y de esta manera optimizar la recuperación metalúrgica de cobre.